smileyCTF2025 :
rev/DNA
Flag : .;,;.{we_ought_to_start_storing_our_data_as_dna_instead}
Description
deoxy ribo nucleic acid deoxy meaning without oxygen ribo meaning the 5-carbon sugar backbone nucleic meaning of the nucleus acid meaning proton donor
Solution
Initial Recon
We start by looking at the challenge directory:
➜ dna ls
main.cpython-310.pyc vm.dna
➜ dna
We can see that this is a virtual machine challenge, and the Python code has been compiled with Python 3.10 into a .pyc file ,Before diving into the challenge, let’s take a moment to understand what a virtual machine (VM) is.
What Is A VM?
VM is short form of Virtual Machine. A virtual machine is exactly what it’s name is, it’s virtual!.
An example of physical machine is your CPU. Your CPU is executing real instructions. When you do a mov instruction, your CPU will take minimum number of steps to complete that instruction. That instruction will have effect on real registers and memory.
When it comes to a virtual CPU (machine), it may or may not have a move instruction in the first place! Even if it has a mov instruction, it’ll be moving data to/from variables declared within the program. So the virtual cpu doesn’t directly use anything real (registers/memory) and all the resources that it’ll use will be stored in a variable that is already allocated on either the stack or the heap. All the (virtual) instructions that a virtual machine will run will ultimately be converted to machine code. Because of this conversion, a virtual CPU takes much more number of steps than a physical CPU to execute a single (virtual) instruction and because of this, virtual machines are slower too.
How Do Virtual Machines Work?
Since a virtual machine is trying to emulate some new instruction set, it’ll need to have a CPU that will be able to decode those set of instructions and for that all virtual machines implement their own virtual CPU. How do we do that? Well, a CPU is just a bunch of registers and some helper units.
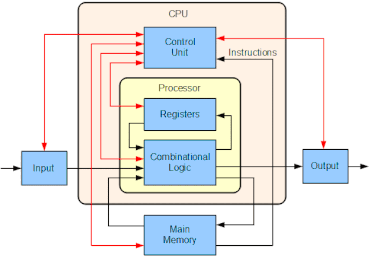
A virtual CPU is much similar to a physical CPU. It’ll have it’s own set of registers and cache and all. A simple implementation in code will look something like this
class RegID(IntEnum):
RAX = 0
RBX = 1
RCX = 2
# Add other registers as needed
class CPU:
def __init__(self, num_registers: int, code_size: int):
self.registers: List[int] = [0] * num_registers # X registers
self.stack: List[int] = []
self.pc: int = 0 # Program counter
self.bytecode: List[int] = [0] * code_size
self.code_sz: int = code_size
# Additional VM components can go here
# e.g., flags, memory, etc.
This makes up the structure of our CPU, but then how will it execute instructions? Normally, challenge developers write their program in a symbolic language and then convert it to the virtual CPUs assembly code. This assembled code is what we refer to as the bytecode. It’s just an array of numbers like the opcodes of your actual CPU.
This bytecode is then read and passed to a Fetch, Decode, Execute (FeDeX) loop. This loop does what it’s name is. It fetches the current instruction from bytecode, decodes what it means (useful part) and then executes it! This is very much similar to what an actual CPU does but this decoding part makes up the extra steps that our virtual CPU has to take.
The FeDeX Loop
In normal CPU, there is a register called the program counter (instruction pointer in Intel CPUs). This register contains an absolute address or an offset from a base address that directly or indirectly points to the next instruction that needs to be executed. So, the fetch part just needs to keep track of this program counter. To fetch the next instruction, the program will do
while pc < len(code):
opcode, operand = map(trans, [code[pc:pc + 2], code[pc + 2:pc + 12]])
# fetch current instruction
match opcode:
# decode
case 0:
# execute
s.append(operand)
pc += 12
this is where the interesting part comes : In all normal, not crazy VMs you’ll find a FeDeX loop like this one. This function is what we need to find if it’s a VM challenge. Generally it’s easy to find because of the code structure here! When you’ll see this code in a graph like format, you’ll notice that almost all similar VMs (with a FeDeX loop) will have similar structure. Let’s try that in this crackme.
Starting with the Challenge
To decompile the .pyc file back into Python source code, I used pylingual.io. and this was the result :
Virtual Machine Overview
import marshal
import sys
s = []
m = {}
nm = {'A': 0, 'T': 1, 'G': 2, 'C': 3}
unlucky = [b'\x8coooooooooooonooolooo,ooo\x9cSooo\x06o\x12o\x1bo\x0bnvo\x13o\x0bmSo\x1bo\x0blvo\x13o\x0bnSo\x1bo\x0bkvo\x13o\x0blSo\x1bo\x0bmvo\x13o\x0bkSo\x13o\x0eo\x0bo<oFj!\xb5n;\xb5n.\xb5n(\xb5n,\xc6n\xb5m\x01\x02\xc6n\xb5l\x1b\x02\x1f\xc6o\x1deooo\x95fS\x1a\x01\x03\x1a\x0c\x04\x16Q\xb5h\x1a\x01\x03\x1a\x0c\x04\x16booo\x9ccoookmcncncncngn', b'\x96uuuuuuuuuuuuruuu}uuu6uuu\x86\x11uuu\x11t\x08u\x11w\x08t\x11v\x08w\x11q\x11p\xf1u\tu1u\xf6t\x08v\tu\tt\tw\x13v1u(n\x08q\x01u\x01t\x01w\xd5v\xd4u\xf6t\xf6t1u(e)w\x08p\x08s\tv\tspulu\x01w\tq\tpluluMuvuIu\x04i\x04g\tv\x14w\x11u&u\\s;\xafq426!\xafq!642\xafq6!24\x16tuuuuuuuuuuuwuuusuuu&uuu\x86ouuu\x1cu\tu(|\x08t\tt\x01u\x01t\xd5w\xd4u\xf6t\xe6w\x04w&u\\u\xdcv\xafv\x06\x00\x18\xafw\x1b\x18\xafs\x03\x14\x19\x00\x10\x06\xdcw\xafw[E\xaft\x16\xdcu\x07xuuu\x8f|I\x00\x1b\x19\x00\x16\x1e\x0cK\xafr\x00\x1b\x19\x00\x16\x1e\x0cnuuu\x86wuuuou\x8fh\x00\x1b\x19\x00\x16\x1e\x0c*G[I\x19\x1a\x16\x14\x19\x06K[I\x11\x1c\x16\x01\x16\x1a\x18\x05K\xdcq\xaf|\x10\x1b\x00\x18\x10\x07\x14\x01\x10\xafs\x06\x1a\x07\x01\x10\x11\x07}uuu\xafq\x1e\x10\x0c\x06\xdcr\xafw\x06D\xafw\x06G\xafw\x06F\xafv\x01\x18\x05\xaft\x06\xaft\x1c\x07yuuu\x07xuuu\x07xuuu\x07{uuu\x07zuuucuuu\x86guuuqwqtqt{t{tmtotw\x8a}w', b"\x8aiiiiiiiiiiiihiiiniiijiii\x9a/iii\x1di\rh\xeah\xe0i\xe1i\xc9h\x1di\rk\xeah\xc9k\rj\rm\xedi\x1dj\xc9m\xc8i\xc8k\xc8hhi.i\xeei\x0fh\rl\ro\xeda\ro\x1dl\xeaj\x14i\x15i\x1dj\xeah\x08j\ri:i@n'\xb3o\x1b\x08\x07\r\x06\x04\xb3`\x0f\x1c\x07\n\x1d\x06\x06\x05\x1a\nkiiiiiiiiiiikiiikiii:iii\x9aaiii\x15i\x15h(i:i@h'\xc0i\xc0k\xb3h\x11\xb3h\x10\x1bliii\x1bliii\x93`U\x1c\x07\x05\x1c\n\x02\x10W\xb3n\x1c\x07\x05\x1c\n\x02\x10Miii\x9akiiiai\x93r\x1c\x07\x05\x1c\n\x02\x106ZGU\x05\x06\n\x08\x05\x1aWGU\x05\x08\x04\x0b\r\x08W\niiiiiiiiiiiiiiiijiiiiiii\x9aCiii\x0ci3h\ri3k\xeei\xeeh\x0fk\rh\rk\xeda3j\xeei\x0fh\rj\rm\xeda3m\xeeimi3l:i@l\x93s\x1c\x07\x05\x1c\n\x02\x106ZGU\x05\x06\n\x08\x05\x1aWG\x1c\x07\x05\x1c\n\x02\x10\nkiiiiiiiiiiimiiiliiiziii\x9a-iii\x1di\xeai\xc9h\x15h\xc8hhi\x1dk\rh\xeah\x14k\xe1h\xc9j\x15k\xc8hhi\x1dm\rk\xeah-i4e\x14j\x15h\x15k\x15jpipi\x15i\rh\x15jpiUi\x18z\ri:i@j'\xb3m(*.=\x80miii\xc0l\xb3l\x1a\x1c\x19\x0c\x1b\xb3a66\x00\x07\x00\x1d66\xb3m\x05\x00\x1a\x1d\xb3n\x1a\x01\x1c\x0f\x0f\x05\x0c\xb3l\x1b\x08\x07\x0e\x0c\xc0m\xb3m\x1a\x0c\x05\x0f\xb3n\x04\x08\x19\x19\x00\x07\x0e\xb3m\x02\x0c\x10\x1a\xb3h\x00\xc0k\xb3`66\n\x05\x08\x1a\x1a66\xb3h\x1b\x1bliii\x1b`iii\x1bciiiOiii\x9aeiiiehahcheh\x7fhm\x96\x93J\x1c\x07\x05\x1c\n\x02\x106ZGU\x05\x06\n\x08\x05\x1aWG\x1c\x07\x05\x1c\n\x02\x10G66\x00\x07\x00\x1d66\nkiiiiiiiiiiiliiiliiiziii\x9a;iii\x1di\rh\xeah\x14k\x1di\rk\xeah\x14j`i\x15k\xc9h\rm\xc8h\x14m\x1dk\xeei\x0fh\rl\ro\xeda\x15j\xc9j\x15m\xc8h\xc9m\xc8i\ri\rn\xeckpi-i\xeah\xeah\x1bA\x1dl\xeai\xc9o\xe1i\xc8h:i\x18`@a'\x1bkiii\xb3n\x01\x08\x1a\x01\x05\x00\x0b=\x80Iiii\nhiiiiiiiiiiikiiimiiiZiii\x9auiii\xe8i\x15i4`\x14h\x15h\x1di\xe1i\xeah\x02k?ihi\x18k\ri:i@h'\xc0h\xb3j\x06\x1b\r\xc0k\xb3kGY\x1bniii\xc0h\xb3j\x02\x0c\x10\x1bliii\x1b`iii\x1bciii[iii\x9amiiik\xe9si\x93P\x1c\x07\x05\x1c\n\x02\x106ZGU\x05\x06\n\x08\x05\x1aWG\x1c\x07\x05\x1c\n\x02\x10G66\x0e\x0c\x1d\x00\x1d\x0c\x0466GU\x05\x06\n\x08\x05\x1aWGU\x0e\x0c\x07\x0c\x11\x19\x1bW\x80hiii\xc0n\xb3c66\x00\x04\x19\x06\x1b\x1d66\xb3`\x1b\x08\x07\r\x0b\x10\x1d\x0c\x1a\xb3j\x08\x05\x05\xb3o\x1a\x01\x08[\\_\xb3o\r\x00\x0e\x0c\x1a\x1d\x1bziii\xb3b66\x0e\x0c\x1d\x00\x1d\x0c\x0466\xc0l\x1bpiii\x1bBiii\xb3m\x01\x05\x00\x0b\xb3m\x1b\x05\x00\x0b\xb3h\x0b\xc0h\x1bwiii\x1bCiii\x1b`iii\x1bciiiDiii\x9agiiiahahkhchAhehk\x94\x93O\x1c\x07\x05\x1c\n\x02\x106ZGU\x05\x06\n\x08\x05\x1aWG\x1c\x07\x05\x1c\n\x02\x10G66\x0e\x0c\x1d\x00\x1d\x0c\x0466\xc0o\xb3a66\x07\x08\x04\x0c66\xb3c66\x04\x06\r\x1c\x05\x0c66\xb3e66\x18\x1c\x08\x05\x07\x08\x04\x0c66\x1b}iii\x1b\\iii\xb3d66\n\x05\x08\x1a\x1a\n\x0c\x05\x0566\x1bliii\xc0h\x1bviii\x1bSiii\x1b`iii\x1bciiiLiii\x9aoiiiaigh}n\x1bciii\xc0o\x1bYiii\xb3m\x1a\x0c\x0c\r\xb3o\x1b\x0c\r\x1c\n\x0c\xb3k\x07\x04\xb3o\x1f\x08\x05\x1c\x0c\x1a\xb3m\r\x00\n\x1d\xc0h\x1bciii\x1bliii\x1b+iii\x1b`iii\x1bciiiHiii\x9aaiiiakwh}hey", b'\x82aaaaaaaaaaaacaaagaaa"aaa\x92]aaa&a\x05`\x05c\xe5a\x05c\x15a\xe2b\x1ca&a\x05b\x05e\xe5a\x05e\x15`\x1da\x05d\xece\x1c`\x15c\x05g\x15`\x15b\xe2`\xfaa\x05f\xfcb\xe2``a\x05a2aHi/\x02aaaaaaaaaaaaaaaabaaaaaaa\x92Iaaa\x04a;`\x05a;c\xe6a\x07`\x05`\x05c\xe5i;b\xe6a\x07`\x05b\x05e\xe5i;e\xe6aea;d2aHd\x9bt\x14\x0f\r\x14\x02\n\x18>UO]\r\x0e\x02\x00\r\x12_O,,\x02eaaaaaaaaaaaeaaagaaaraaa\x92saaa\x15a\xe2a\xc1`\x1da\x1d`\x1dc\x1db\xc0e2aH`/\xc8c\xbbd\x12\x14\x11\x04\x13\xbbf>>\x0f\x04\x16>>\xc8e\xbbb\x02\r\x12\xbbe\x0f\x00\x0c\x04\xbbd\x03\x00\x12\x04\x12\xbbb\x05\x02\x15\xc8`\xbbh>>\x02\r\x00\x12\x12>>\xc8a\x9bh]\x14\x0f\r\x14\x02\n\x18_\xbbf\x14\x0f\r\x14\x02\n\x18Zaaa\x92caaas`\x9b|\x14\x0f\r\x14\x02\n\x18>UO]\r\x0e\x02\x00\r\x12_O,,O>>\x0f\x04\x16>>\x02`aaaaaaaaaaafaaadaaa~aaa\x92\x05aaa\x15a\xe2a\x0b`\x1d`\x08a\x1dc\xc5`\xef`\x1cb\x15c\x1db\xc1b\xc0a\xe2`\x1ce\x1de\x05a\x05a\x05`\xe4bxa\x1de\x05c\x05a\x05`\xe4bxava\x1ce\x15e\x15d\x1db\xc1g\xc0a\xe2`\xe2`%a<k=c\x1cd\x1cg\x1de\x1ddxa\x1db\x1dg]a\x10D\x1db2aHb/\x88caaa\x88`aaa\xc8f\x13gaaa\xbbi>>\x02\x00\r\r>>\xbbe\r\x08\x12\x15\xbbg\x17\x00\r\x14\x04\x12\xbbh\x04\x0f\x14\x0c\x04\x13\x00\x15\x04\xbbg\x12\x0e\x13\x15\x04\x05\xbbe\n\x04\x18\x12\xc8f\x13haaa\xbbe\x00\x13\x06\x12\xbbg\n\x16\x00\x13\x06\x12\xbbi\x08\x0f\x12\x15\x00\x0f\x02\x04\xbbe\x17\x00\r\x12\xbb`\x08\xbb`\n\x13laaa\x13naaa\x13qaaa\x13paaa_aaa\x92maaas`m`}`y`o`e`\x9b\x7f\x14\x0f\r\x14\x02\n\x18>UO]\r\x0e\x02\x00\r\x12_O,,O>>\x02\x00\r\r>>\xc8g\xbbi>>\x0f\x00\x0c\x04>>\xbbk>>\x0c\x0e\x05\x14\r\x04>>\xbbm>>\x10\x14\x00\r\x0f\x00\x0c\x04>>\x13faaa\x13yaaa\xbbl>>\x02\r\x00\x12\x12\x02\x04\r\r>>\x13naaa\x13naaa\x13laaa\x13qaaa\x13paaa[aaa\x92gaaaiam`ub\xbbc,,\x02aaaaaaaaaaaaaaaa`aaa!aaa\x92maaa\x04a;`\x05a;c\x05`2aHc\x9bt\x14\x0f\r\x14\x02\n\x18>UO]\r\x0e\x02\x00\r\x12_O,%/\xc8b\x13Iaaa\x13Haaa\x13Kaaa\x13naaa\x13naaa\x13naaa\x13qaaa\x13paaa\'aaa\x92eaaaiae`\xbbc,%\xc8`\xbbh\x0c\x04\x15\x00\x02\r\x00\x12\x12\x9b@\x06\r\x0e\x03\x00\r\x12IH:F\x0f\x14\x02\r\x04\x0e\x15\x08\x05\x04>\x0c\x00\x11F<A\\A,%I\x9b`H\xc8e\xbbe\x15\x18\x11\x04\xbbe\x05\x08\x02\x15\xbbe\x04\x19\x04\x02\xbbc\x0f\x0c\xc8c\x13Laaa\x13Saaa\x13naaa\x13naaa\x13qaaa\x13paaaVaaa\x92gaaaqbumyb']
trans = lambda s: sum((nm[c] << 2 * i for i, c in enumerate(s)))
if len(sys.argv)!= 2:
opcodent(f'Usage: {sys.argv[0]} <dna_file>')
sys.exit(1)
code = open(sys.argv[1]).read()
flag = input('> ').encode()
if len(flag)!= 56:
exit('WRONG!')
if flag[:6]!= b'.;,;.{':
exit('WRONG!')
if flag[(-1)]!= 125:
exit('WRONG!')
flag = flag[6:(-1)]
for i in range(len(flag)):
m[640 + i] = flag[i]
pc = 0
The code defines two key data structures:
s: An array used internally by the VM as stack (we’ll understand why later).
m: A dictionary that serves as memory for the virtual machine.
DNA Code Representation
The virtual machine reads a DNA-like string from a file, which consists only of the characters {A, T, G, C}. Here’s an example:
GAAAAGGAAAAAAAGGGTAAAAAAGTGATAAGGAAAAAAACGTAAAAAAAGTGAGAAGGAAAAAAAACAGAAAAAAGTGACAAGGAAAAAAAGGAGAAAAAAGTGAATAGGAAAAAAAACGTAAAAAA...
To decode these characters into numbers, a simple base-4 mapping is used:
nm = {'A': 0, 'T': 1, 'G': 2, 'C': 3}
This mapping turns each DNA character into a digit between 0 and 3. DNA to Integer Conversion
The VM uses the following trans lambda function to convert short DNA strings into integers:
trans = lambda s: sum((nm[c] << 2 * i for i, c in enumerate(s)))
This treats the DNA string as a little-endian base-4 number.
Example:
trans('AT') = (0 << 0) + (1 << 2) = 0 + 4 = 4
The unlucky List
The unlucky list contains 4 elements, each being a long bytes object with repetitive patterns at the beginning (ooo..., uuu..., iii..., aaa...). Initially, it’s unclear what these represent.
unlucky = [
b'\x8coooooooooooonooolooo,ooo\x9cSooo...', # Element 0
b'\x96uuuuuuuuuuuuruuu}uuu6uuu\x86\x11uuu...', # Element 1
b"\x8aiiiiiiiiiiiihiiiniiijiii\x9a/iii...", # Element 2
b'\x82aaaaaaaaaaaacaaagaaa"aaa\x92]aaa...' # Element 3
]
When we examine its usage in case 13, the purpose becomes clear:
case 13: # CALL_SNIPPET
if not s:
raise Exception('Stack underflow')
key = s.pop() # Get decryption key from stack
print(m[666])
print(f'Key: {key}')
def f():
return
# XOR decrypt with the key
decrypted_bytes = bytes([b ^ key for b in unlucky.pop(0)])
# Convert decrypted bytes to Python code object
f.__code__ = marshal.loads(decrypted_bytes)
# Execute the hidden code
f()
pc += 2
The key insight is the use of marshal.loads() on the decrypted bytes and its assignment to f.__code__. This pattern strongly suggests that the unlucky list contains XOR-encrypted Python bytecode. The repetitive patterns at the beginning of each element are likely artifacts of this XOR encryption process.
- Popping a decryption key from the execution stack
- XOR decrypting each byte in the current unlucky element with this key
- Using
marshal.loads()to convert the decrypted bytes back into Python bytecode - Dynamically executing the revealed code by replacing a dummy function’s bytecode
This is a sophisticated obfuscation technique that hides the actual program logic until runtime. The marshal.loads() → f.__code__ pattern clearly indicates we’re dealing with compiled Python bytecode rather than just encrypted data. Each of the 4 elements likely contains a different stage of the program’s execution, consumed sequentially via unlucky.pop(0).
Input Validation and Setup
The program expects a DNA code file as an argument. It reads the file and prompts the user for a flag.
if len(sys.argv) != 2:
print(f'Usage: {sys.argv[0]} <dna_file>')
sys.exit(1)
code = open(sys.argv[1]).read()
flag = input('> ').encode()
Flag Validation
The flag must meet strict format requirements:
if len(flag) != 56:
exit('WRONG!')
if flag[:6] != b'.;,;.{':
exit('WRONG!')
if flag[-1] != 125: # ASCII code for '}'
exit('WRONG!')
After validation, the wrapper format is stripped, leaving 49 bytes of core flag data:
flag = flag[6:-1]
Storing the Flag in VM Memory
Each byte of the flag is stored in the virtual memory dictionary m, starting at address 640:
for i in range(len(flag)):
m[640 + i] = flag[i]
Beginning Execution
The virtual machine sets the program counter (pc) to 0 and begins a decode-execute loop:
pc = 0
while pc < len(code):
# Each instruction is 12 DNA characters:
# - First 2 characters: opcode
# - Next 10 characters: operand
opcode, operand = map(trans, [code[pc:pc + 2], code[pc + 2:pc + 12]])
...
Opcode Interpretation
PUSH — Opcode 0
case 0: # PUSH
# Push operand onto the stack
s.append(operand)
pc += 12
and here we confirm that s is the stack
POP — Opcode 1
case 1: # POP
# Remove the top element from the stack
if not s:
raise Exception('Stack underflow')
s.pop()
pc += 2
LOAD — Opcode 2
case 2: # LOAD from memory
# Push value at memory[operand] onto the stack
if operand not in m:
raise Exception(f'Uninitialized memory access at {operand}')
s.append(m[operand])
pc += 12
STORE — Opcode 3
case 3: # STORE to memory
# Pop top of stack and store at memory[operand]
if not s:
raise Exception('Stack underflow')
m[operand] = s.pop()
pc += 12
ADD — Opcode 4
case 4: # ADD
# Pop two values, push their sum
if len(s) < 2:
raise Exception('Stack underflow')
a, b = s.pop(), s.pop()
s.append(a + b)
pc += 2
SUB — Opcode 5
case 5: # SUB
# Pop two values, push b - a
if len(s) < 2:
raise Exception('Stack underflow')
a, b = s.pop(), s.pop()
s.append(b - a)
pc += 2
MUL — Opcode 6
case 6: # MUL
# Pop two values, push their product
if len(s) < 2:
raise Exception('Stack underflow')
a, b = s.pop(), s.pop()
s.append(a * b)
pc += 2
MOD — Opcode 7
case 7: # MOD
# Pop two values, push b % a (a must not be 0)
if len(s) < 2:
raise Exception('Stack underflow')
a, b = s.pop(), s.pop()
if a == 0:
raise Exception('Division by zero')
s.append(b % a)
pc += 2
EQUAL — Opcode 8
case 8: # EQUAL
# Push 1 if a == b else 0
if len(s) < 2:
raise Exception('Stack underflow')
a, b = s.pop(), s.pop()
print(a)
print(b)
s.append(1 if a == b else 0)
pc += 2
JMP — Opcode 9
case 9: # JMP
# Unconditional jump to address `operand`
pc = operand
JMP_IF_EQ_1 — Opcode 10
case 10: # JMP_IF_EQ_1
# Conditional jump if top of stack == 1
if not s:
raise Exception('Stack underflow')
if s.pop() == 1:
pc = operand
else:
pc += 12
JMP_IF_NEQ_1 — Opcode 11
case 11: # JMP_IF_NEQ_1
# Conditional jump if top of stack != 1
if not s:
raise Exception('Stack underflow')
if s.pop() != 1:
pc = operand
else:
pc += 12
PRINT — Opcode 12
case 12: # PRINT
# Print character from top of stack
if not s:
raise Exception('Stack underflow')
print(chr(s.pop()), end='')
pc += 2
CALL_SNIPPET — Opcode 13
case 13: # CALL_SNIPPET
# Decrypt and execute marshaled code from 'unlucky' list
if not s:
raise Exception('Stack underflow')
key = s.pop()
def f(): return
f.__code__ = marshal.loads(bytes([b ^ key for b in unlucky.pop(0)]))
f()
pc += 2
SWAP — Opcode 14
case 14: # SWAP
# Swap values in the nm (DNA map)
if len(s) < 2:
raise Exception('Stack underflow')
a, b = s.pop(), s.pop()
if a not in nm or b not in nm:
raise Exception('Invalid swap keys')
nm[a], nm[b] = nm[b], nm[a]
pc += 2
HALT — Opcode 15
case 15: # HALT
# Stop execution
break
When running the VM with a test flag of the required 56-character length, the program crashes at the first CALL_SNIPPET instruction:
$ python3 v1.py vm.dna
> .;.,;{the_secret_dna_koy_is_hiooon_horo_1234567890123aa}
Traceback (most recent call last):
File "v1.py", line 116, in <module>
f.__code__ = marshal.loads(bytes([b ^ key for b in unlucky.pop(0)]))
ValueError: bad marshal data (unknown type code)
After seeing this error, it suggests that the key is wrong. Let’s examine where the key comes from. Looking at the assembly code before the crash:
015202: LOAD_MEM Operand=666
015214: CALL_SNIPPET
The LOAD_MEM with operand 666 means m[666] is pushed to the stack, then when CALL_SNIPPET executes key = s.pop(), this becomes our decryption key. So the key is input-determined.
To find the valid key, we need to understand the memory layout:
- Flag bytes are stored starting at memory address 640
- Flag format removes the first 6 characters (
.;,;.{) - Therefore:
key = m[666] = flag[666 - 640 + 6] = flag[32]
Since we need to find the valid key that should be at m[666], we must brute force to find the correct character for flag[32].
Brute Force Key Recovery
Since the key must be a valid ASCII character (0-255), we can brute force all possible keys:
for key in range(256):
try:
decrypted = bytes([b ^ key for b in unlucky[0]])
obj = marshal.loads(decrypted)
print(f"Key {key} ({chr(key)}): Success - {type(obj)}")
if isinstance(obj, types.CodeType):
dis.dis(obj)
except:
continue
Result: The correct key is 111 (ASCII ‘o’)
This means flag[26] should be ‘o’ for the first bytecode to decrypt properly.
Systematic Approach
Since unlucky.pop(0) consumes elements sequentially, we need to:
- Determine the correct key for
unlucky[0]→flag[26] = 'o' - Update the flag and continue execution to find the key for
unlucky[1] - Repeat for all four bytecode snippets
Decompiled Python Code from unlucky Bytecode
unlucky[0]
Python Bytecode:
15 0 BUILD_MAP 0
2 STORE_FAST 0 (tmp)
16 4 LOAD_GLOBAL 0 (nm)
6 LOAD_CONST 1 ('T')
8 BINARY_SUBSCR
10 LOAD_FAST 0 (tmp)
12 LOAD_CONST 2 ('A')
14 STORE_SUBSCR
17 16 LOAD_GLOBAL 0 (nm)
18 LOAD_CONST 3 ('G')
20 BINARY_SUBSCR
22 LOAD_FAST 0 (tmp)
24 LOAD_CONST 1 ('T')
26 STORE_SUBSCR
18 28 LOAD_GLOBAL 0 (nm)
30 LOAD_CONST 4 ('C')
32 BINARY_SUBSCR
34 LOAD_FAST 0 (tmp)
36 LOAD_CONST 3 ('G')
38 STORE_SUBSCR
19 40 LOAD_GLOBAL 0 (nm)
42 LOAD_CONST 2 ('A')
44 BINARY_SUBSCR
46 LOAD_FAST 0 (tmp)
48 LOAD_CONST 4 ('C')
50 STORE_SUBSCR
20 52 LOAD_FAST 0 (tmp)
54 STORE_GLOBAL 0 (nm)
56 LOAD_CONST 0 (None)
58 RETURN_VALUE
Decompiled Function:
def unlucky0():
tmp = {}
tmp['A'] = nm['T'] # A gets T's value
tmp['T'] = nm['G'] # T gets G's value
tmp['G'] = nm['C'] # G gets C's value
tmp['C'] = nm['A'] # C gets A's value
nm = tmp # Replace global nm mapping
unlucky[1]
Python Bytecode:
24 0 LOAD_CONST 1 ('AGCT')
2 STORE_FAST 0 (s1)
25 4 LOAD_CONST 2 ('TCAG')
6 STORE_FAST 1 (s2)
26 8 LOAD_CONST 3 ('CTGA')
10 STORE_FAST 2 (s3)
27 12 LOAD_CONST 4 (<code object unlucky at 0x...>)
14 LOAD_CONST 5 ('unlucky_2.<locals>.<dictcomp>')
16 MAKE_FUNCTION 0
18 LOAD_FAST 0 (s1)
20 GET_ITER
22 CALL_FUNCTION 1
24 STORE_FAST 3 (tmp)
28 26 LOAD_FAST 0 (s1)
28 LOAD_FAST 1 (s2)
30 LOAD_FAST 2 (s3)
32 BUILD_TUPLE 3
34 GET_ITER
>> 36 FOR_ITER 27 (to 92)
38 STORE_FAST 4 (s)
29 40 LOAD_GLOBAL 0 (enumerate)
42 LOAD_GLOBAL 1 (sorted)
44 LOAD_GLOBAL 2 (nm)
46 LOAD_METHOD 3 (keys)
48 CALL_METHOD 0
50 CALL_FUNCTION 1
52 CALL_FUNCTION 1
54 GET_ITER
>> 56 FOR_ITER 16 (to 90)
58 UNPACK_SEQUENCE 2
60 STORE_FAST 5 (i)
62 STORE_FAST 6 (c)
30 64 LOAD_FAST 3 (tmp)
66 LOAD_FAST 6 (c)
68 DUP_TOP_TWO
70 BINARY_SUBSCR
72 LOAD_GLOBAL 2 (nm)
74 LOAD_FAST 4 (s)
76 LOAD_FAST 5 (i)
78 BINARY_SUBSCR
80 BINARY_SUBSCR
82 INPLACE_SUBTRACT
84 ROT_THREE
86 STORE_SUBSCR
88 JUMP_ABSOLUTE 28 (to 56)
29 >> 90 JUMP_ABSOLUTE 18 (to 36)
31 >> 92 LOAD_FAST 3 (tmp)
94 STORE_GLOBAL 2 (nm)
96 LOAD_CONST 0 (None)
98 RETURN_VALUE
Decompiled Python Code:
def unlucky1(nm_in):
s1 = "AGCT"
s2 = "TCAG"
s3 = "CTGA"
total = sum(nm_in.values())
tmp = {c: total for c in s1}
for s in (s1, s2, s3):
for i, c in enumerate(sorted(nm_in.keys())):
tmp[c] -= nm_in[s[i]]
return tmp
unlucky[2]
Python Bytecode:
35 0 LOAD_GLOBAL 0 (__import__)
2 LOAD_CONST 1 ('random')
4 CALL_FUNCTION 1
6 STORE_DEREF 0 (r)
36 8 LOAD_DEREF 0 (r)
10 LOAD_METHOD 1 (seed)
8 12 LOAD_GLOBAL 0 (__import__)
14 LOAD_CONST 2 ('functools')
16 CALL_FUNCTION 1
18 LOAD_METHOD 2 (reduce)
20 LOAD_CONST 3 (<code object unlucky at 0x...>)
22 LOAD_CONST 4 ('unlucky_3.<locals>.<lambda>')
24 MAKE_FUNCTION 0
26 LOAD_GLOBAL 3 (nm)
28 LOAD_METHOD 4 (values)
30 CALL_METHOD 0
32 CALL_METHOD 2
34 CALL_METHOD 1
36 POP_TOP
37 38 LOAD_BUILD_CLASS
40 LOAD_CLOSURE 0 (r)
42 BUILD_TUPLE 1
44 LOAD_CONST 5 (<code object unlucky at 0x...>)
46 LOAD_CONST 6 ('unlucky')
48 MAKE_FUNCTION 8 (closure)
50 LOAD_CONST 6 ('unlucky')
52 LOAD_GLOBAL 5 (dict)
54 CALL_FUNCTION 3
56 STORE_FAST 0 (unlucky)
53 58 LOAD_FAST 0 (unlucky)
60 LOAD_GLOBAL 3 (nm)
62 CALL_FUNCTION 1
64 STORE_GLOBAL 3 (nm)
66 LOAD_CONST 0 (None)
68 RETURN_VALUE
Decompiled Python Code:
def unlucky2(nm_in):
seed = 0
for v in nm_in.values():
seed ^= v
random.seed(seed)
class Unlucky(dict):
def __init__(self, mapping):
super().__init__(mapping)
keys = list("ACGT")
random.shuffle(keys)
for i in range(4):
self["ACGT"[i]] = mapping[keys[i]]
new_nm = Unlucky(nm_in)
return new_nm
unlucky[3]
Python Bytecode:
58 0 LOAD_BUILD_CLASS
2 LOAD_CONST 1 (<code object unlucky at 0x...>)
4 LOAD_CONST 2 ('MM')
6 MAKE_FUNCTION 0
8 LOAD_CONST 2 ('MM')
10 LOAD_GLOBAL 0 (type)
12 CALL_FUNCTION 3
14 STORE_FAST 0 (MM)
70 16 LOAD_BUILD_CLASS
18 LOAD_CONST 3 (<code object unlucky at 0x...>)
20 LOAD_CONST 4 ('MD')
22 MAKE_FUNCTION 0
24 LOAD_CONST 4 ('MD')
26 LOAD_GLOBAL 1 (dict)
28 LOAD_FAST 0 (MM)
30 LOAD_CONST 5 (('metaclass',))
32 CALL_FUNCTION_KW 4
34 STORE_FAST 1 (MD)
73 36 LOAD_GLOBAL 2 (exec)
38 LOAD_CONST 6 ("globals()['nucleotide_map'] = MD(")
40 LOAD_GLOBAL 1 (dict)
42 LOAD_GLOBAL 3 (nm)
44 CALL_FUNCTION 1
46 FORMAT_VALUE 0
48 LOAD_CONST 7 (')')
50 BUILD_STRING 3
52 CALL_FUNCTION 1
54 POP_TOP
56 LOAD_CONST 0 (None)
58 RETURN_VALUE
Decompiled Python Code:
def unlucky3(nm_in):
class MM(type):
def __new__(cls, name, bases, dct):
return super().__new__(cls, name, bases, dct)
def __call__(cls, *args, **kwargs):
instance = super().__call__(*args, **kwargs)
vals = list(instance.values())
vals = vals[::2] + vals[1::2]
for i, k in enumerate(sorted(instance.keys())):
instance[k] = vals[i]
return instance
class MD(dict, metaclass=MM):
pass
new_nm = MD(dict(nm_in))
return new_nm
print("Initial nm:", nm)
nm = unlucky0(nm)
print("After unlucky0, nm =", nm)
nm = unlucky1(nm)
print("After unlucky1, nm =", nm)
nm = unlucky2(nm)
print("After unlucky2, nm =", nm)
nm = unlucky3(nm)
print("After unlucky3, nm =", nm)
Output
Initial nm: {'A': 0, 'T': 1, 'G': 2, 'C': 3}
After unlucky0, nm = {'A': 1, 'T': 2, 'G': 3, 'C': 0}
After unlucky1, nm = {'A': 3, 'G': 2, 'C': 1, 'T': 0}
After unlucky2, nm = {'A': 2, 'G': 1, 'C': 3, 'T': 0}
After unlucky3, nm = {'A': 2, 'G': 1, 'C': 3, 'T': 0}
Explanation
- Initial nm: The starting nucleotide map is
{'A': 0, 'T': 1, 'G': 2, 'C': 3}. - After unlucky0: The nucleotide map is updated based on the first transformation function.
- After unlucky1: The nucleotide map is further transformed using the second function.
- After unlucky2: The third transformation function applies additional changes.
- After unlucky3: The final transformation function is applied, resulting in the final nucleotide map.
Each function (unlucky0, unlucky1, unlucky2, unlucky3) modifies the global nm variable, and the changes are printed after each step.
Before starting to write the assembler, I manually verified the state of the nm mapping after each CALL instruction (opcode 13). This was done by checking the operand of the LOAD instruction preceding each CALL. Below are the results of the dynamic disassembly:
➜ sol awk '/CALL/ { print lines[NR-1]; print } { lines[NR] = $0 }' asm.txt
=== DYNAMIC DISASSEMBLY ===
DEBUG: After CALL #1, nm updated to: {'A': 1, 'T': 2, 'G': 3, 'C': 0}
DEBUG: After CALL #1, nm updated to: {'A': 1, 'T': 2, 'G': 3, 'C': 0}
DEBUG: After CALL #2, nm updated to: {'A': 3, 'G': 2, 'C': 1, 'T': 0}
DEBUG: After CALL #2, nm updated to: {'A': 3, 'G': 2, 'C': 1, 'T': 0}
DEBUG: After CALL #3, nm updated to: {'A': 2, 'G': 1, 'C': 3, 'T': 0}
DEBUG: After CALL #3, nm updated to: {'A': 2, 'G': 1, 'C': 3, 'T': 0}
DEBUG: After CALL #4, nm updated to: {'A': 2, 'G': 1, 'C': 3, 'T': 0}
==================================================
Nucleotide mappings change after each CALL instruction
15202: LOAD GGTGGAAAAA (666) ; debug marker [nm: A=0,T=1,G=2,C=3]
15214: CALL ; will change nucleotide mapping [nm: A=0,T=1,G=2,C=3]
30418: LOAD GTATTCCCCC (667) ; flag[27] [nm: A=1,T=2,G=3,C=0]
30430: CALL ; will change nucleotide mapping [nm: A=1,T=2,G=3,C=0]
45634: LOAD GCCGGTTTTT (662) ; flag[22] [nm: A=3,T=0,G=2,C=1]
45646: CALL ; will change nucleotide mapping [nm: A=3,T=0,G=2,C=1]
60850: LOAD GTAAATTTTT (673) ; flag[33] [nm: A=2,T=0,G=1,C=3]
60862: CALL ; will change nucleotide mapping [nm: A=2,T=0,G=1,C=3]
Total instructions: 9844
CALL operations: 4
➜ sol
Based on the disassembly:
m[640 + 26] = 111(ASCII for ‘o’)m[640 + 27] = 117(ASCII for ‘u’)m[640 + 22] = 105(ASCII for ‘i’)m[640 + 33] = 97(ASCII for ‘a’)
flag[26]=111
flag[27]=117
flag[22]=105
flag[33]=97
Next Steps
Using the above observations, I will proceed to write the assembler, ensuring that the dynamic changes to the nm mapping are accounted for at each step.
python disassembler
import sys
from typing import List, Tuple, Dict
class DynamicDNADisassembler:
def __init__(self):
self.initial_nm = {'A': 0, 'T': 1, 'G': 2, 'C': 3}
self.instructions = {
0: "PUSH",
1: "POP",
2: "LOAD",
3: "STORE",
4: "ADD",
5: "SUB",
6: "MUL",
7: "MOD",
8: "EQ",
9: "JMP",
10: "JEQ",
11: "JNE",
12: "PRINT",
13: "CALL",
14: "SWAP",
15: "HALT"
}
self.mapping_transforms = {
111: {'A': 1, 'T': 2, 'G': 3, 'C': 0},
117: {'A': 3, 'G': 2, 'C': 1, 'T': 0},
105: {'A': 2, 'G': 1, 'C': 3, 'T': 0}
}
self.predefined_values = {22: 105, 26: 111, 27: 117}
def trans(self, dna_sequence: str, nm: Dict[str, int]) -> int:
return sum((nm[c] << 2 * i for i, c in enumerate(dna_sequence)))
def reverse_trans(self, value: int, length: int) -> str:
nucleotides = ['A', 'T', 'G', 'C']
result = []
for i in range(length):
result.append(nucleotides[(value >> (2 * i)) & 3])
return ''.join(result)
def predict_call_key(self, instructions_so_far: List, current_stack: List[int]) -> int:
for addr, instr, operand_dna, operand in reversed(instructions_so_far[-10:]):
if instr == "LOAD" and operand in self.predefined_values:
return self.predefined_values[operand]
return None
def disassemble_dynamic(self, code: str) -> List[Tuple[int, str, str, int, Dict[str, int]]]:
instructions = []
pc = 0
current_nm = self.initial_nm.copy()
call_count = 0
while pc < len(code):
if pc + 2 > len(code):
break
opcode_dna = code[pc:pc + 2]
opcode = self.trans(opcode_dna, current_nm)
if opcode in [1, 4, 5, 6, 7, 8, 12, 13, 14, 15]:
operand_dna = ""
operand = 0
instruction_length = 2
else:
if pc + 12 > len(code):
break
operand_dna = code[pc + 2:pc + 12]
operand = self.trans(operand_dna, current_nm)
instruction_length = 12
instr_name = self.instructions.get(opcode, f"UNKNOWN_{opcode}")
instructions.append((pc, instr_name, operand_dna, operand, current_nm.copy()))
if instr_name == "CALL":
call_count += 1
predicted_key = None
if call_count == 1:
predicted_key = 111
elif call_count == 2:
predicted_key = 117
elif call_count >= 3:
predicted_key = 105
if predicted_key and predicted_key in self.mapping_transforms:
current_nm = self.mapping_transforms[predicted_key].copy()
print(f"DEBUG: After CALL #{call_count}, nm updated to: {current_nm}")
pc += instruction_length
return instructions
def format_instruction_dynamic(self, addr: int, instr: str, operand_dna: str,
operand: int, nm: Dict[str, int], call_count: int = 0) -> str:
addr_str = f"{addr:04d}"
nm_str = f"[nm: A={nm['A']},T={nm['T']},G={nm['G']},C={nm['C']}]"
if operand_dna:
base_str = f"{addr_str}: {instr:<8} {operand_dna} ({operand})"
if instr in ["LOAD", "STORE"]:
if operand == 666:
base_str += " ; debug marker"
elif operand >= 640 and operand < 696:
base_str += f" ; flag[{operand-640}]"
elif operand in [22, 26, 27]:
value = self.predefined_values.get(operand, "unknown")
base_str += f" ; predefined value={value}"
return f"{base_str} {nm_str}"
else:
if instr == "CALL":
return f"{addr_str}: {instr:<8} ; will change nucleotide mapping {nm_str}"
return f"{addr_str}: {instr} {nm_str}"
def disassemble_file_dynamic(self, filename: str) -> str:
try:
with open(filename, 'r') as f:
code = f.read().strip()
except FileNotFoundError:
return f"Error: File '{filename}' not found"
except Exception as e:
return f"Error reading file: {e}"
instructions = self.disassemble_dynamic(code)
if not instructions:
return "No valid instructions found"
output_lines = []
output_lines.append("Dynamic DNA Virtual Machine Disassembly")
output_lines.append("=" * 50)
output_lines.append("Nucleotide mappings change after each CALL instruction")
output_lines.append("")
call_count = 0
for addr, instr, operand_dna, operand, nm in instructions:
if instr == "CALL":
call_count += 1
output_lines.append(self.format_instruction_dynamic(addr, instr, operand_dna, operand, nm, call_count))
output_lines.append("")
output_lines.append(f"Total instructions: {len(instructions)}")
output_lines.append(f"CALL operations: {call_count}")
return "\n".join(output_lines)
def analyze_mapping_evolution(self, code: str) -> Dict:
instructions = self.disassemble_dynamic(code)
mapping_states = []
call_positions = []
for addr, instr, operand_dna, operand, nm in instructions:
if instr == "CALL":
call_positions.append(addr)
mapping_states.append((addr, nm.copy()))
return {
'mapping_evolution': mapping_states,
'call_positions': call_positions,
'total_calls': len(call_positions)
}
def main():
if len(sys.argv) != 2:
print(f"Usage: {sys.argv[0]} <dna_bytecode_file>")
sys.exit(1)
disassembler = DynamicDNADisassembler()
print("=== DYNAMIC DISASSEMBLY ===")
result = disassembler.disassemble_file_dynamic(sys.argv[1])
print(result)
if __name__ == "__main__":
main()
the results instructions was good especially that we had exactly 4 call instructions
Total instructions: 9844
CALL operations: 4
To reverse the VM instructions, we begin by analyzing the repeated structure of the first few lines. Here’s a representative snippet:
0000: LOAD AAAGGAAAAA (640) ; flag[0] [nm: A=0,T=1,G=2,C=3]
0012: PUSH GGGTAAAAAA (106) [nm: A=0,T=1,G=2,C=3]
0024: MUL [nm: A=0,T=1,G=2,C=3]
0026: LOAD TAAGGAAAAA (641) ; flag[1] [nm: A=0,T=1,G=2,C=3]
0038: PUSH CGTAAAAAAA (27) [nm: A=0,T=1,G=2,C=3]
0050: MUL [nm: A=0,T=1,G=2,C=3]
0052: LOAD GAAGGAAAAA (642) ; flag[2] [nm: A=0,T=1,G=2,C=3]
0064: PUSH ACAGAAAAAA (140) [nm: A=0,T=1,G=2,C=3]
0076: MUL [nm: A=0,T=1,G=2,C=3]
0078: LOAD CAAGGAAAAA (643) ; flag[3] [nm: A=0,T=1,G=2,C=3]
0090: PUSH GGAGAAAAAA (138) [nm: A=0,T=1,G=2,C=3]
0102: MUL [nm: A=0,T=1,G=2,C=3]
0104: LOAD ATAGGAAAAA (644) ; flag[4] [nm: A=0,T=1,G=2,C=3]
0116: PUSH ACGTAAAAAA (108) [nm: A=0,T=1,G=2,C=3]
0128: MUL [nm: A=0,T=1,G=2,C=3]
0130: LOAD TTAGGAAAAA (645) ; flag[5] [nm: A=0,T=1,G=2,C=3]
0142: PUSH CGTTAAAAAA (91) [nm: A=0,T=1,G=2,C=3]
0154: MUL [nm: A=0,T=1,G=2,C=3]
0156: LOAD GTAGGAAAAA (646) ; flag[6] [nm: A=0,T=1,G=2,C=3]
0168: PUSH CAAGAAAAAA (131) [nm: A=0,T=1,G=2,C=3]
0180: MUL [nm: A=0,T=1,G=2,C=3]
0182: LOAD CTAGGAAAAA (647) ; flag[7] [nm: A=0,T=1,G=2,C=3]
0194: PUSH GGAGAAAAAA (138) [nm: A=0,T=1,G=2,C=3]
0206: MUL [nm: A=0,T=1,G=2,C=3]
0208: LOAD AGAGGAAAAA (648) ; flag[8] [nm: A=0,T=1,G=2,C=3]
0220: PUSH GGGTAAAAAA (106) [nm: A=0,T=1,G=2,C=3]
0232: MUL [nm: A=0,T=1,G=2,C=3]
0234: LOAD TGAGGAAAAA (649) ; flag[9] [nm: A=0,T=1,G=2,C=3]
0246: PUSH CCCTAAAAAA (127) [nm: A=0,T=1,G=2,C=3]
0258: MUL [nm: A=0,T=1,G=2,C=3]
0260: LOAD GGAGGAAAAA (650) ; flag[10] [nm: A=0,T=1,G=2,C=3]
0272: PUSH TAGGAAAAAA (161) [nm: A=0,T=1,G=2,C=3]
0284: MUL [nm: A=0,T=1,G=2,C=3]
0286: LOAD CGAGGAAAAA (651) ; flag[11] [nm: A=0,T=1,G=2,C=3]
0298: PUSH CACTAAAAAA (115) [nm: A=0,T=1,G=2,C=3]
0310: MUL [nm: A=0,T=1,G=2,C=3]
...
Instruction Semantics:
LOAD (addr) – pushes the value at memory[addr] (i.e., flag[i]) onto the stack.
PUSH (val) – pushes a constant coefficient onto the stack.
MUL – pops two values, multiplies them, and pushes the result.
This forms flag[i] × Cj[i].
This pattern of LOAD, PUSH, MUL repeats 49 times, suggesting a coefficient vector Cj of length 49.
Following that, we see a sequence of ADD instructions:
1274: ADD [nm: A=0,T=1,G=2,C=3]
1276: ADD [nm: A=0,T=1,G=2,C=3]
1278: ADD [nm: A=0,T=1,G=2,C=3]
1280: ADD [nm: A=0,T=1,G=2,C=3]
1282: ADD [nm: A=0,T=1,G=2,C=3]
1284: ADD [nm: A=0,T=1,G=2,C=3]
1286: ADD [nm: A=0,T=1,G=2,C=3]
1288: ADD [nm: A=0,T=1,G=2,C=3]
1290: ADD [nm: A=0,T=1,G=2,C=3]
1292: ADD [nm: A=0,T=1,G=2,C=3]
1294: ADD [nm: A=0,T=1,G=2,C=3]
1296: ADD [nm: A=0,T=1,G=2,C=3]
1298: ADD [nm: A=0,T=1,G=2,C=3]
1300: ADD [nm: A=0,T=1,G=2,C=3]
1302: ADD [nm: A=0,T=1,G=2,C=3]
1304: ADD [nm: A=0,T=1,G=2,C=3]
1306: ADD [nm: A=0,T=1,G=2,C=3]
1308: ADD [nm: A=0,T=1,G=2,C=3]
1310: ADD [nm: A=0,T=1,G=2,C=3]
1312: ADD [nm: A=0,T=1,G=2,C=3]
1314: ADD [nm: A=0,T=1,G=2,C=3]
1316: ADD [nm: A=0,T=1,G=2,C=3]
1318: ADD [nm: A=0,T=1,G=2,C=3]
1320: ADD [nm: A=0,T=1,G=2,C=3]
1322: ADD [nm: A=0,T=1,G=2,C=3]
1324: ADD [nm: A=0,T=1,G=2,C=3]
...
There are 48 ADD instructions, which cumulatively reduce the 49 products to a single sum.
Thus, each block of operations computes:
$$ \sum_{i=0}^{48} \text{flag}[i] \times C_j[i] $$
This entire process is repeated 49 times, meaning the index j ranges from 0 to 48. For each repetition, a new coefficient vector Cj is used, so we must extract all 49 coefficient vectors C₀, C₁, …, C₄₈.
i wrote this parser to exctract them all
import re
def parse_assembly_equations(assembly_lines):
equations = []
current_constants = []
in_sequence = False
load_count = 0
prev_instruction = None
for line in assembly_lines:
match = re.match(r'^\d+:\s*(\w+)\s*(?:([A-Z]+\s*\(\d+\))|\(\d+\))?', line.strip())
if not match:
continue
instruction = match.group(1)
if instruction == 'LOAD' and not in_sequence:
in_sequence = True
load_count = 1
current_constants = []
elif in_sequence and instruction == 'PUSH':
value = match.group(2)
if value:
constant = re.search(r'\((\d+)\)', value).group(1)
current_constants.append(constant)
elif in_sequence and instruction == 'LOAD':
load_count += 1
elif in_sequence and instruction == 'ADD':
prev_instruction = 'ADD'
elif in_sequence and instruction == 'STORE' and prev_instruction == 'ADD':
if load_count == len(current_constants) and load_count == 49:
equation = f"sum_{{i=0}}^{{48}} flag[i] × J[i], where J[i] = [{', '.join(current_constants)}]"
eq_number_match = re.search(r'\((\d+)\)', line)
if eq_number_match:
eq_number = int(eq_number_match.group(1))
equations.append((eq_number, equation))
else:
print(f"Warning: Could not find equation number in line: {line}")
in_sequence = False
prev_instruction = 'STORE'
elif in_sequence and instruction == 'LOAD' and prev_instruction != 'STORE':
if load_count == len(current_constants) and load_count == 49:
equation = f"sum_{{i=0}}^{{48}} flag[i] × J[i], where J[i] = [{', '.join(current_constants)}]"
equations.append((None, equation))
in_sequence = False
load_count = 1
current_constants = []
prev_instruction = 'LOAD'
else:
prev_instruction = instruction
return equations
with open('asm.txt', 'r') as f:
lines = f.readlines()
equations = parse_assembly_equations(lines)
print(len(equations), "equations found:")
for eq_number, eq in equations:
print(f"Equation stored at {eq_number}: {eq}")
Coefficient Vectors (Cj)
The coefficient vectors (Cj) of length 49 for each j ranging from 0 to 48 were extracted. These coefficients are stored in memory starting at address 4096, with each vector occupying 4 consecutive memory slots. Below is the result:
Memory Layout for Coefficient Vectors
memory[4096]tomemory[4096 + 4 * 48]contain the coefficients for all 49 equations.
Example Coefficients
Here are some of the extracted coefficient vectors:
C₀ (memory[4096]):
[106, 27, 140, 138, 108, 91, 131, 138, 106, 127, 161, 115, 177, 152, 15, 55, 230, 131, 147, 183, 235, 197, 200, 104, 188, 196, 118, 28, 21, 97, 151, 217, 118, 22, 212, 31, 101, 227, 155, 237, 146, 68, 75, 71, 218, 173, 41, 220, 161]C₁ (memory[4100]):
[56, 249, 152, 225, 66, 136, 113, 243, 63, 233, 254, 69, 191, 1, 147, 169, 118, 97, 193, 175, 25, 141, 234, 105, 9, 53, 115, 162, 104, 104, 153, 57, 11, 28, 3, 146, 14, 70, 154, 102, 169, 66, 133, 29, 107, 155, 22, 231, 61]C₂ (memory[4104]):
[149, 104, 66, 72, 140, 134, 140, 174, 236, 10, 209, 162, 15, 223, 191, 183, 77, 137, 106, 69, 54, 1, 122, 195, 62, 99, 155, 10, 18, 117, 164, 216, 231, 150, 255, 127, 193, 145, 190, 34, 46, 64, 189, 182, 27, 163, 156, 156, 150]
…
C₄₈ (memory[4288]):
[10, 177, 31, 35, 108, 132, 53, 119, 122, 72, 51, 62, 160, 167, 251, 191, 245, 142, 79, 235, 184, 142, 194, 218, 240, 66, 226, 179, 125, 18, 246, 234, 25, 56, 4, 240, 215, 214, 42, 143, 32, 87, 5, 215, 62, 231, 179, 186, 219]Each coefficient vector is used in one of the 49 equations.
The equations are structured as:
$$ \sum_{i=0}^{48} \text{flag}[i] \times C_j[i] $$
where `Cj` is the coefficient vector for the j-th equation.
Memory Addressing
- The coefficient vectors are stored sequentially in memory:
C₀starts atmemory[4096]C₁starts atmemory[4100]- …
C₄₈starts atmemory[4288]
This structure ensures that all 49 equations can be efficiently computed using the stored coefficients.
Observations## Target Values Extraction
After decrypting the bytecode, we need to find the target values that the VM is checking against. The assembly shows a pattern of comparisons:
67774: LOAD TTTTTTGTTT (4096) [nm: A=2,T=0,G=1,C=3]
67786: PUSH TCATCCTAAA (692012) [nm: A=2,T=0,G=1,C=3]
67798: EQ [nm: A=2,T=0,G=1,C=3]
67800: LOAD TGTTTTGTTT (4100) [nm: A=2,T=0,G=1,C=3]
67812: PUSH AGGCATGGGA (611030) [nm: A=2,T=0,G=1,C=3]
67824: EQ [nm: A=2,T=0,G=1,C=3]
… (continuing with similar patterns) …
68996: LOAD TCCATTGTTT (4284) [nm: A=2,T=0,G=1,C=3]
69008: PUSH AAACAGATAA (665322) [nm: A=2,T=0,G=1,C=3]
69020: EQ [nm: A=2,T=0,G=1,C=3]
69022: LOAD TTTCTTGTTT (4288) [nm: A=2,T=0,G=1,C=3]
69034: PUSH GATATAGCAA (710793) [nm: A=2,T=0,G=1,C=3]
69046: EQ [nm: A=2,T=0,G=1,C=3]
The pattern shows:
LOADinstruction loads a value from memory at the specified addressPUSHinstruction pushes a target value onto the stackEQcompares the two values and pushes 1 if equal, 0 otherwise
target_values = {
4096: 692012,
4100: 611030,
4104: 658676,
4108: 556679,
4112: 588728,
4116: 628470,
4120: 659130,
4124: 623012,
4128: 590356,
4132: 670831,
4136: 734960,
4140: 694096,
4144: 673431,
4148: 676517,
4152: 638313,
4156: 730305,
4160: 651347,
4164: 612947,
4168: 614037,
4172: 722768,
4176: 662232,
4180: 608720,
4184: 598699,
4188: 626932,
4192: 659018,
4196: 554138,
4200: 627484,
4204: 620929,
4208: 655810,
4212: 598103,
4216: 664749,
4220: 772833,
4224: 710796,
4228: 669747,
4232: 576742,
4236: 715958,
4240: 682073,
4244: 687276,
4248: 806029,
4252: 660519,
4256: 728567,
4260: 689664,
4264: 746796,
4268: 597800,
4272: 629625,
4276: 585142,
4280: 678960,
4284: 665322,
4288: 710793
}
Verification Logic
There are 49 equality checks that compare loaded values with pushed values. Each comparison pushes either 1 (if equal) or 0 (if not equal) onto the stack.
After finishing all comparisons, the code adds all 49 values on the stack:
69048: ADD [nm: A=2,T=0,G=1,C=3]
69050: ADD [nm: A=2,T=0,G=1,C=3]
69052: ADD [nm: A=2,T=0,G=1,C=3]
69054: ADD [nm: A=2,T=0,G=1,C=3]
69056: ADD [nm: A=2,T=0,G=1,C=3]
...
69138: ADD [nm: A=2,T=0,G=1,C=3]
69140: ADD [nm: A=2,T=0,G=1,C=3]
69142: ADD [nm: A=2,T=0,G=1,C=3]
If all comparisons return 1, then: 1 + 1 + 1 + ... + 1 = 49 (correct flag)
Otherwise, the sum will be less than 49 (incorrect flag).
69144: PUSH GTCTTTTTTT (49) [nm: A=2,T=0,G=1,C=3]
69156: EQ [nm: A=2,T=0,G=1,C=3]
69158: JNE TCCAACTTGT (69308) [nm: A=2,T=0,G=1,C=3]
Output Messages
If sum ≠ 49 (jumps to 69308):
Prints “WRONG!” - ASCII values [87, 82, 79, 78, 71, 33]
>>> k = [87, 82, 79, 78, 71, 33]
>>> "".join([chr(i) for i in k])
'WRONG!'
If sum = 49:
Prints “CORRECT!” - ASCII values [67, 79, 82, 82, 69, 67, 84, 33]
>>> k = [67, 79, 82, 82, 69, 67, 84, 33]
>>> "".join([chr(i) for i in k])
'CORRECT!'
Success Path Assembly
69170: PUSH CTTGTTTTTT (67) [nm: A=2,T=0,G=1,C=3] # 'C'
69182: PRINT [nm: A=2,T=0,G=1,C=3]
69184: PUSH CCTGTTTTTT (79) [nm: A=2,T=0,G=1,C=3] # 'O'
69196: PRINT [nm: A=2,T=0,G=1,C=3]
69198: PUSH ATGGTTTTTT (82) [nm: A=2,T=0,G=1,C=3] # 'R'
69210: PRINT [nm: A=2,T=0,G=1,C=3]
69212: PUSH ATGGTTTTTT (82) [nm: A=2,T=0,G=1,C=3] # 'R'
69224: PRINT [nm: A=2,T=0,G=1,C=3]
69226: PUSH GGTGTTTTTT (69) [nm: A=2,T=0,G=1,C=3] # 'E'
69238: PRINT [nm: A=2,T=0,G=1,C=3]
69240: PUSH CTTGTTTTTT (67) [nm: A=2,T=0,G=1,C=3] # 'C'
69252: PRINT [nm: A=2,T=0,G=1,C=3]
69254: PUSH TGGGTTTTTT (84) [nm: A=2,T=0,G=1,C=3] # 'T'
69266: PRINT [nm: A=2,T=0,G=1,C=3]
69268: PUSH GTATTTTTTT (33) [nm: A=2,T=0,G=1,C=3] # '!'
69280: PRINT [nm: A=2,T=0,G=1,C=3]
69282: PUSH AATTTTTTTT (10) [nm: A=2,T=0,G=1,C=3] # '\n'
69294: PRINT [nm: A=2,T=0,G=1,C=3]
69296: JMP ACGTCCTTGT (69406) [nm: A=2,T=0,G=1,C=3]
Failure Path Assembly
69308: PUSH CGGGTTTTTT (87) [nm: A=2,T=0,G=1,C=3] # 'W'
69320: PRINT [nm: A=2,T=0,G=1,C=3]
69322: PUSH ATGGTTTTTT (82) [nm: A=2,T=0,G=1,C=3] # 'R'
69334: PRINT [nm: A=2,T=0,G=1,C=3]
69336: PUSH CCTGTTTTTT (79) [nm: A=2,T=0,G=1,C=3] # 'O'
69348: PRINT [nm: A=2,T=0,G=1,C=3]
69350: PUSH ACTGTTTTTT (78) [nm: A=2,T=0,G=1,C=3] # 'N'
69362: PRINT [nm: A=2,T=0,G=1,C=3]
69364: PUSH CGTGTTTTTT (71) [nm: A=2,T=0,G=1,C=3] # 'G'
69376: PRINT [nm: A=2,T=0,G=1,C=3]
69378: PUSH GTATTTTTTT (33) [nm: A=2,T=0,G=1,C=3] # '!'
69390: PRINT [nm: A=2,T=0,G=1,C=3]
69392: PUSH AATTTTTTTT (10) [nm: A=2,T=0,G=1,C=3] # '\n'
69404: PRINT [nm: A=2,T=0,G=1,C=3]
69406: HALT [nm: A=2,T=0,G=1,C=3]
Solving a System of Linear Equations
Problem Formulation
We are given a system of equations of the form: $$\sum_{j=0}^{48} \text{flag}[j] \cdot C_j[i] = m[i] \quad \text{for } i = 0, 1, \dots, 48$$
This can be interpreted as a matrix equation: $$\mathbf{C} \cdot \mathbf{f} = \mathbf{m}$$
Where:
- $\mathbf{C}$ is a $49 \times 49$ matrix, with $C_j[i]$ representing the coefficient in row $i$, column $j$
- $\mathbf{f}$ is a column vector of length 49 representing the flag values: $[\text{flag}[0], \text{flag}[1], \dots, \text{flag}[48]]^T$
- $\mathbf{m}$ is the column vector of resulting values: $[m[0], m[1], \dots, m[48]]^T$
Solution Methodology
to solve the System: we now need to solve:
$$ \mathbf{C} \cdot \mathbf{f} = \mathbf{m} $$
To find $\mathbf{f}$ (i.e., the flag):
- Exact Arithmetic (e.g., Modular Inverse) :
$$ \mathbf{f} = \mathbf{C}^{-1} \cdot \mathbf{m} \mod 256 $$
Step 3: Verify System Solvability
To ensure that the 49 equations are linearly independent, we verify the determinant of the coefficient matrix $\mathbf{C}$. If the determinant is non-zero, the system has a unique solution.
>>> np.linalg.det(A)
7.002684569518382e+123
Since $\det(\mathbf{C}) \neq 0$, matrix $\mathbf{C}$ is invertible and the system can be solved directly.
Implementation
The following Python script solves the system:
import numpy as np
# Construct coefficient matrix and target vector
addrs = sorted(memory.keys())
A = np.vstack([memory[a] for a in addrs])
b = np.array([m[a] for a in addrs], dtype=float)
# Solve the linear system
try:
f = np.linalg.solve(A, b)
print("Matrix A is invertible, proceeding with direct solve.")
method = "direct solve"
except np.linalg.LinAlgError:
# Fallback to least-squares if matrix is singular
f, residuals, rank, s = np.linalg.lstsq(A, b, rcond=None)
method = f"least-squares (rank {rank})"
# Convert to integer values
f_int = np.rint(f).astype(int)
# Display results
print(f"Solution method: {method}")
print("Flag bytes:", f_int.tolist())
print("As ASCII:", ''.join(chr(v) for v in f_int))
if 'residuals' in locals():
print("Residual norm²:", residuals)
Results
The solution yields the following flag values:
Flag bytes: [119, 101, 95, 111, 117, 103, 104, 116, 95, 116, 111, 95, 115, 116, 97, 114, 116, 95, 115, 116, 111, 114, 105, 110, 103, 95, 111, 117, 114, 95, 100, 97, 116, 97, 95, 97, 115, 95, 100, 110, 97, 95, 105, 110, 115, 116, 101, 97, 100]
ASCII representation: we_ought_to_start_storing_our_data_as_dna_instead
The direct matrix solution method successfully recovered the flag, demonstrating that the system was well-conditioned and had a unique solution.